Simple Harmonic Vibration, Simple Harmonic Motion 단순 조화 진동, 단순 조화 운동 | (2025-01-20) |
단조화 진동, 단조화 운동, 단 진동, Simple Oscillator, 단순 진동자, 단순조화운동 조화운동 비교 | |
▷
Top
▷
기초과학
▷
물리
▷
운동(학)
▷
대표적인 운동
▷ Top ▷ 진동/파동 ▷ 진동 ▷ 진동(조화운동)
▷ Top ▷ 진동/파동 ▷ 진동 ▷ 진동(조화운동)
1. `단순 조화운동`, `조화운동` 비교 ㅇ 단순 조화 운동/진동 (Simple Harmonic Motion/Vibration, SHM) - 고유 주파수를 갖고, 정현적으로 움직이는, 가장 단순한 형태의 진동 * (운동 형태) . 일정 주기로 같은 운동을 되풀이하는 단순한 운동 .. 평형점을 중심으로, 양쪽 방향으로 왕복하는, 작은 진동 운동 . 외력이 한번 만 작용하고, 이후 마찰력 (감쇄) 없이, 일정한 에너지로 단순 반복 운동을 함 * (변위 형태) . 변위가 시간의 조화함수로 표현됨 .. 즉, 조화적 시간 의존성을 갖음 .. 시간에 대해 정현 또는 여현 함수 형태의 변위로 기술되는 주기적 과정 * (용어) . 때론, 무감쇠 진동(Undamped Vibration)/비감쇠 자유 진동(Undamped Free Vibration) 라고함 ㅇ 조화 진동/운동 (Harmonic Vibration/Motion) - 모든 조화진동은 단조화 진동이 여러 형태로 중첩된 현상으로 봄 ☞ 조화파 참조 2. 단조화 운동의 특징 ㅇ 힘의 관점에서, - 작용하는 힘(복원력)이, ☞ 탄성복원력 참조 . 항상 하나의 중심 고정점을 향하고, . 그 크기가 중심 고정점으로부터의 거리(변위)에 비례함 ㅇ 단순함 - 여러 진동중에서도 가정 단순하고 기본적인 것이 단조화 파동(진동)임 . 주기성(진동 주파수)이 운동의 진폭에 무관 ☞ 단진자, 등시성 참조 . 시간에 대해 삼각함수 형태의 변위를 갖음 ☞ 삼각함수 참조 . 운동을 억제하는 손실이 없음 ☞ 보존력, 비보존력 참조 3. 단조화 운동의 例) 단순 진동자(Simple Oscillator) ㅇ 역학적 진동 : 용수철 진자(Spring Pendulum), 중력 진자(Gravitational Pendulum) 등 ㅇ 전기 진동 : 병렬 공진회로 등 ※ 특히, 복잡한 진동계의 일차 근사(선형 근사)로써 유용함 - 복원력이 변위에 만 비례 . 例) F = - k x = m a ☞ 후크의 법칙 참조 - 질량(관성)이 일정 - 운동을 감쇠시키는 손실이 없는 등 ☞ 비감쇠 자유 진동 참조 4. (단)조화 운동의 수학적 표현 : (운동방정식) ㅇ 상수계수를 갖는 선형 2계 미분방정식 ☞ 조화진동 운동방정식, 2차 운동방정식 참조 - 단조화운동을 나타내는 미분방정식 :- 단조화운동 미분방정식 해 :
ㅇ 조화진동 관련 운동방정식 및 해(解) ☞ 단순 조화 운동방정식 참조 5. 원운동, 단조화운동의 유사성 ※ (원운동) → (단순조화진동) ㅇ 반지름 A → 진폭 A ㅇ 각 변위 θ=ωt → 위상 변위 θ=ωt ㅇ 각속도 ω= dθ/dt → 각진동수 ω=2πf ㅇ 회전수 f → 진동수 f = 1/T
※ 운동표현식 : y(t) = A sin ωt, x(t) = A cos ωt - 속도 최대값 :
- 가속도 최대값 :
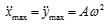
▷대표적인 운동
1. 자유 낙하 운동 2. 포물선 운동 3. 단순 조화 운동
▷진동(조화운동)
1. 단순 조화진동 2. 조화진동 3. 단조화 운동방정식 4. 기본 주파수 5. 결합(Coupling) 6. 결합 진동 7. 맥놀이 8. 비감쇠 자유 진동 9. 모드 해석 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]