Ensemble 앙상블 | (2025-02-08) |
Ensemble Average, 앙상블 평균, 집합 평균, Statistical Average, 통계적 평균 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
신호 표현/성질
▷
평균화
▷ Top ▷ 기초과학 ▷ 수학 ▷ 확률/통계 ▷ 확률 과정 ▷ 랜덤과정 용어
▷ Top ▷ 기초과학 ▷ 수학 ▷ 확률/통계 ▷ 확률 과정 ▷ 랜덤과정 용어
1. 앙상블 (Ensemble) 이란?
ㅇ 영어 뜻으로는, `함께,동시에,통일,조화` 등을 의미
- 例) "함께 조화를 이뤄냄" ☞ 기계학습에서, 앙상블 방법 등
ㅇ [확률통계] 앙상블 : { X(t, ξ) }
- 랜덤 프로세스의 결과로써 나올 수 있는 모든 멤버들의 모음/집단
. 결국, `랜덤 프로세스에 관한 모든 정보를 갖고 있는 총합`을 의미
* [참고] ☞ `표본 랜덤변수 랜덤과정 앙상블 비교` 참조
2. [확률통계] 앙상블 멤버 (Ensemble Member) 이란?
ㅇ 앙상블 멤버 / 표본 함수 : X(t, ξ)
- 랜덤 프로세스의 결과 하나 하나에 대응될 수 있는 표본 시간 함수
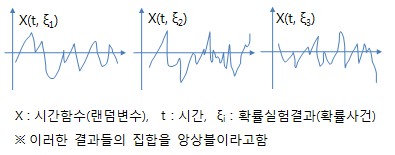 ※ 한편, 이러한 앙상블에 대해, 아래와 같이 평균적 특성을 살펴보는 것이 바람직할 때가 많음
3. [확률통계] 앙상블 평균 (또는, 통계적 평균, 집합 평균) : (고정된 시점에 초점을 맞춤)
ㅇ 시간 t에서 랜덤과정 X(t)의 `기대값(평균)`
- 정상과정 하의 특정 시간 t에서,
. 모든 가능한 시행 결과값들의 기대값(평균)
- 즉, 확률실험에서 나올 수 있는 모든 가능한 결과값들의 평균
ㅇ `앙상블 평균 (1차 모멘트)`
[# μ_X(t) = E[X(t)] = \int^{\infty}_{-\infty} x f_X(x,t)dx #]
ㅇ `앙상블 분산 (2차 모멘트)`
[# σ^2_X(t) = E[\left(X(t)-μ_X(t)\right)^2] = \int^{\infty}_{-\infty} \left(x(t)-μ_X(t)\right)^2 f_X(x,t)dx #]
※ 랜덤과정에서, 앙상블 평균,앙상블 분산은,
- 시간에 따라서 변할 수 있는 시간의 함수가 됨
ㅇ 서로다른 두 시점에서 앙상블의 유사성(상관성) => `자기상관`
[# R_X(t_1,t_2) = E[X_1(t)X_2(t)] = \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} x_1x_2 f_{X_1X_2}(x_1,t_1;x_2,t_2) \, dx_1dx_2 #]
- {#R_X(t_1,t_2)#} : 자기상관함수
- {#f_{X_1X_2}(x_1,t_1;x_2,t_2)#} : 결합 확률밀도함수
4. [확률통계] 시간 평균 : (시간적 변화에 만 관심을 갖음)
ㅇ 일반적으로, 결정신호에 대한 비확률적인 시간 평균을 주로 지칭하나,
ㅇ 여기서는, 어떤 앙상블 맴버(표본 함수) 중 하나를 취하고,
시간 평균을 구한 것을 말함
ㅇ 시간 평균의 기호
[# < x(t) > = \lim_{T \rightarrow \infty} \frac{1}{T} \int^{T/2}_{-T/2} x^2(t) \, dt #]
5. [확률통계] 에르고딕성 이란? : ( 앙상블 평균 = 시간 평균 )
ㅇ 정상상태 과정 (랜덤과정의 통계적 성질이 시간에 따라 변하지 않음) 하에서,
- 집단 전체에 대한 시간 평균과 앙상블 평균이 같아지는 성질
※ 한편, 이러한 앙상블에 대해, 아래와 같이 평균적 특성을 살펴보는 것이 바람직할 때가 많음
3. [확률통계] 앙상블 평균 (또는, 통계적 평균, 집합 평균) : (고정된 시점에 초점을 맞춤)
ㅇ 시간 t에서 랜덤과정 X(t)의 `기대값(평균)`
- 정상과정 하의 특정 시간 t에서,
. 모든 가능한 시행 결과값들의 기대값(평균)
- 즉, 확률실험에서 나올 수 있는 모든 가능한 결과값들의 평균
ㅇ `앙상블 평균 (1차 모멘트)`
[# μ_X(t) = E[X(t)] = \int^{\infty}_{-\infty} x f_X(x,t)dx #]
ㅇ `앙상블 분산 (2차 모멘트)`
[# σ^2_X(t) = E[\left(X(t)-μ_X(t)\right)^2] = \int^{\infty}_{-\infty} \left(x(t)-μ_X(t)\right)^2 f_X(x,t)dx #]
※ 랜덤과정에서, 앙상블 평균,앙상블 분산은,
- 시간에 따라서 변할 수 있는 시간의 함수가 됨
ㅇ 서로다른 두 시점에서 앙상블의 유사성(상관성) => `자기상관`
[# R_X(t_1,t_2) = E[X_1(t)X_2(t)] = \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} x_1x_2 f_{X_1X_2}(x_1,t_1;x_2,t_2) \, dx_1dx_2 #]
- {#R_X(t_1,t_2)#} : 자기상관함수
- {#f_{X_1X_2}(x_1,t_1;x_2,t_2)#} : 결합 확률밀도함수
4. [확률통계] 시간 평균 : (시간적 변화에 만 관심을 갖음)
ㅇ 일반적으로, 결정신호에 대한 비확률적인 시간 평균을 주로 지칭하나,
ㅇ 여기서는, 어떤 앙상블 맴버(표본 함수) 중 하나를 취하고,
시간 평균을 구한 것을 말함
ㅇ 시간 평균의 기호
[# < x(t) > = \lim_{T \rightarrow \infty} \frac{1}{T} \int^{T/2}_{-T/2} x^2(t) \, dt #]
5. [확률통계] 에르고딕성 이란? : ( 앙상블 평균 = 시간 평균 )
ㅇ 정상상태 과정 (랜덤과정의 통계적 성질이 시간에 따라 변하지 않음) 하에서,
- 집단 전체에 대한 시간 평균과 앙상블 평균이 같아지는 성질
▷평균화
1. 평균이란? 2. 산술 평균 3. 기하 평균 4. 조화 평균 5. 가중 평균 6. 이동 평균 7. 가중 이동평균 8. 시간 평균 9. 앙상블 평균 10. 기대값 11. 복합 연평균성장률
▷랜덤과정 용어
1. 결정론적/비결정론적 2. 랜덤 3. 랜덤 변수 4. 표본 함수 5. 앙상블, 앙상블 평균 6. 표본 랜덤변수 랜덤과정 앙상블 비교 7. 독립 항등 분포(iid) 8. 독립 증분 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]