Weibull Distribution 와이블 분포 | (2023-09-04) |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
확률 모형,분포
▷
연속확률분포
1. 와이블 분포 ㅇ 지수분포를 보다 일반화시켜, 여러 다양한 확률분포 형태를 모두 나타낼 수 있도록 고안됨 - 특히, 신뢰성 분야의 응용에서 자주 사용되는 수명 분포 ㅇ 스웨덴 물리학자 W. Weibull가 재료의 파괴강도를 설명하기 위해 1939년에 제안 - "A Statistical Theory of the Strength of Materials" 2. 와이블 분포와 다른 분포와의 관계 ㅇ 2 또는 3개의 모수에 의해 특징지워짐 - 형상모수 : β . β < 1 : 감마분포 . β = 1 : 지수분포 . β = 2 : 레일리히 분포 . β = 3.5 : 정규분포에 근사적 - 척도모수 : η - 위치모수 : γ 3. 와이블 분포 특징 ㅇ 확률밀도함수 - 2 모수(형상모수 β,척도모수 η) 와이블 분포- 3 모수(형상모수 β,척도모수 η,위치모수 γ) 와이블 분포
ㅇ 평균(기대값) - 2 모수(형상모수 β,척도모수 η)
- 3 모수(형상모수 β,척도모수 η)
ㅇ 분산 - 2 모수(형상모수 β,척도모수 η) 및 3 모수(형상모수 β,척도모수 η)
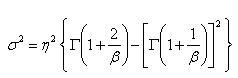
▷연속확률분포
1. 연속 확률분포 요약 2. 연속 균등분포 3. Rayleigh 분포 4. Rician 분포 5. 감마 분포 6. 베타 분포 7. 지수 분포 8. 얼랑 분포 9. 와이블 분포 10. 카이제곱 분포(χ² 분포) 11. t 분포 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]