Orthogonal Coordinate System 직교 좌표계 | (2021-06-02) |
직교 좌표, Orthogonal Coordinate System Transformation, 직교 좌표계 변환, 직교 좌표 변환 | |
▷
Top
▷
기초과학
▷
수학
▷
기초수학
▷
좌표계
1. 직교 좌표계 (Orthogonal Coordinate System) ㅇ 각각의 축 또는 축평면이 직교성을 유지하는 좌표계 - 좌표축이 미리 정해진, 일반적으로 사용되는 좌표계 ㅇ 특징 - 좌표축이 미리 정해짐 - 각각의 축이 상호 독립적인 직교성(직각성)을 갖음 - 통상, 3개의 성분으로 나타냄 (한편, 극좌표계는 2개 성분으로 나타냄) 2. 직교 좌표계 종류 ㅇ 직교 카트시안 좌표계 (일명, 직각 좌표계) - 각각의 축이 직각으로 만남 . 3개의 좌표축은 3개의 좌표평면을 결정하고, . 이것이 공간을 8개의 팔분 공간으로 나눔 ㅇ 직교 곡선 좌표계 : 극좌표계, 확장된 극좌표계 (원통 좌표계, 구 좌표계) 등 - 각각의 축이 직각은 아니지만, 상호 독립적인 직교성을 갖음 3. 직교 좌표계 변환 (Orthogonal Coordinate System Transformation) ㅇ 직각좌표계 ~ 원통좌표계 변환 - 변수 관계식- 변환 관계식
ㅇ 직각좌표계 ~ 구좌표계 변환 - 변수 관계식
- 변환 관계식
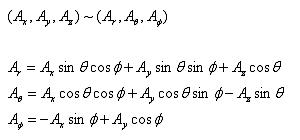
▷좌표계
1. 좌표계 2. 직교 좌표계 3. 직각 좌표계 4. 극 좌표계 5. 원통 좌표계 6. 구 좌표계 7. 기저벡터 좌표계 8. 경로 좌표계 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]