First-order Circuit 1차 회로, 1차 과도 회로, RC 회로, RL 회로 | (2022-08-10) |
일차 회로 | |
▷
Top
▷
전기전자공학
▷
회로해석
▷
과도 해석 (시간응답)
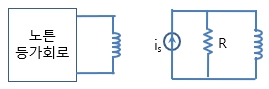
1. 1차 회로 (First-order Circuit) ㅇ 단지 하나의 에너지 저장요소(C 또는 L) 만을 포함하는 회로 - 즉, 커패시터 또는 인덕터가 1개 만 있는 회로 (RC 회로 또는 RL 회로) ※ [참고] ☞ 1차 RC 회로의 특성, 1차 시스템 참조 2. 1차 회로의 방정식 표현 ㅇ 1계 미분방정식으로 표현됨[# \frac{dy(t)}{dt} + a y(t) = f(t) #]- 출력 (미지 함수) : y(t) - 입력 (구동 함수) : f(t) - 미분항 최고 계수(order) : 1계 또는 1차 ㅇ 1계 미분방정식의 해 - 영입력 응답인 경우 (즉, 입력이 없을 때 f(t) = 0), (출력은, 미지 함수의 해)[# y' + ay = 0 \\ y = y_0 e^{-at} = y_0 e^{-t/τ} #]. a (=1/τ, τ: 시정수) : 지수적 감소 또는 증가 .. (RC 회로 시정수 : τ = RC, RL 회로 시정수 : τ = L/R) 3. 1차 회로의 `해` 및 `응답` 비교 ㅇ 선형 미분방정식 해 : 일반해 = 동차해 + 특수해 ㅇ 회로 응답 : 완전응답 = 과도응답 + 강제응답 = (무 입력전원 해) + (입력전원에 따른 부가적인 해) ※ 여기서, - 과도응답 항(項) : 동차해 (homogeneous solution) - 강제응답 항(項) : 특수해 (particaular solution) 4. 1차 회로의 등가 회로 例 ※ 모든 1차 회로는, 테브난 정리,노튼 정리에 의해, 다음 2개 등가 회로로 표현 가능 - 테브난 정리 : 1개 독립 전압원과 1개 등가 저항이 직렬 연결된 등가 회로로 표현 가능 - 노튼 정리 : 1개 독립 전류원과 1개 등가 저항이 병렬 접속된 등가 회로로 표현 가능 ㅇ 테브난 정리에 의한 등가 회로ㅇ 노튼 정리에 의한 등가 회로
▷과도 해석 (시간응답)
1. 시간 응답 2. 정상상태 응답 3. 과도 응답 4. 시정수 5. 0차 유지 6. 1차 회로 (RL, RC) 7. 1차 RC 회로의 특성 8. 2차 회로 (RLC) 9. RC 위상 천이 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]