Laplace Transform Pair 라플라스 변환쌍 | (2021-03-13) |
▷
Top
▷
신호/시스템
▷
변환 해석
▷
라플라스 변환
1. 라플라스 변환쌍 (Laplace Transform Pair) ㅇ 임펄스 함수[# δ(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad 1 #]ㅇ 상수 (t≥0 일 때)[# c \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{c}{s} #]ㅇ 계단 함수, 경사 함수, 포물선 함수[# u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{1}{s} \\ t\;u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{1}{s^2} \\ t^2\;u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{2}{s^3} \\ t^n\;u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{n!}{s^{n+1}} #]ㅇ 지수 함수[# e^{-at}\;u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{1}{s+a} \\ t\;e^{-at}\;u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{1}{(s+a)^2} \\ t^n\;e^{-at}\;u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{n!}{(s+a)^{n+1}} #]ㅇ 삼각 함수[# \sin ωt\;u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{ω}{s^2+ω^2} \\ \cos ωt\;u(t) \quad \stackrel{\small{L}}{\longleftrightarrow} \quad \frac{s}{s^2+ω^2} #]ㅇ 미분ㅇ 기타 유용한 변환쌍 (t≥0 일 때)
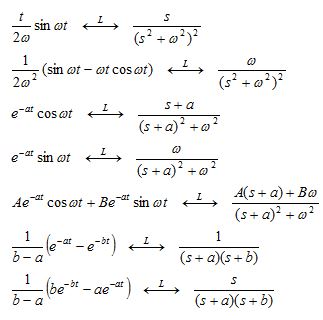
▷라플라스 변환
1. 라플라스 변환 2. 복소 주파수 3. 라플라스 변환쌍 4. 라플라스 변환 성질 5. 라플라스 변환 가능 6. 부분분수 전개 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]