Impulse Function, Impulse Signal, Dirac Delta Function, Unit Delta Function, Kronecker Delta, Unit Sample Sequence 임펄스 함수, 디렉 델타 함수, 임펄스 신호, 임펄스 수열, 크로네커 델타 함수 | (2024-08-23) |
충격 함수, Unit Impulse Function, 단위 임펄스 함수, 단위 임펄스 신호 | |
▷
Top
▷
신호/시스템
▷
신호 표현/성질/종류
▷
신호 파형 종류
1. [함수] 임펄스 함수 = 디렉 델타 함수 ㅇ t = 0 에서 폭이 0 이며 무한대 크기를 갖고, 그 이외에서 크기가 0 이고,[# δ(t) = \left\{ \begin{array}{ll} \infty & (t=0) \\ 0 & (t≠0) \end{array} \right. #]ㅇ 전체 면적은 1 임[# \int^{\infty}_{-\infty} δ(t) dt = 1 #]ㅇ 사실상, 함수라기 보다는 분포(distribution) 또는 일반화 함수(generalized function) 임 - 즉, 함수 자체에 값을 부여할 수 있는 보통의 함수와 달리, 함수 값의 분포를 나타냄 . 따라서, 다른 함수와의 적분 등 연산과 관련될 때 만 그 의미가 있음[# \int^{\infty}_{-\infty} δ(t)f(t) dt = f(0) #]- 결국, 한 순간에서만 무한의 값을 갖고, 나머지에서는 0 인 일종의 일반화된 분포 함수 ㅇ 비록, 잘못된 명칭이긴 하지만, - 임펄스 함수(impulse function), 델타 함수(delta function), 디랙 델타 함수(Dirac delta function) 등 함수라고 표현하는 용어를 흔히 사용 함 ※ 영국의 이론물리학자 디렉(Paul Adrien Maurice Dirac,1933년 노벨물리학상)이 정의한 바 있음 2. [선형대수] 크로네커 델타 함수 ㅇ 디렉 델타 함수의 이산형(離散型)※ 레오폴드 크로네커 (Leopold Kronecker,1823~1891) : 독일 태생의 수학자 3. [이산시간] 임펄스 수열 ㅇ 이산시간 임펄스(discrete-time impulse) 또는 단위 샘플 수열(unit sample sequence) 또는 단위 임펄스수열 (unit impulse sequence) 등 으로 불리움
ㅇ 이산시간 마다 나타나는, 임의 수열을 임펄스 수열로 표현 가능
- 즉, 모든 수열은 단위 임펄스 수열 δ[n]을 상수배(크기 조정) x[k]하고 지연시킨 수열 δ[n-k]들의 합으로 표현 가능 4. [성질] 임펄스 함수의 성질 ㅇ 우함수 특성 - δ(t) = δ(-t) . 좌우 대칭 ㅇ 이동 특성(Shifting) 또는 샘플링 특성(Sampling)
- 이동특성 : 함수 g(t)를 g(t0)로 이동시킴 - 샘플링특성 : 모든 t에 대해 g(t)δ(t-t0)의 적분값은 단지 t=t0 점에서의 함수값 g(t0)로 샘플링한 것과 같음 ㅇ 복제 특성 - g(t) * δ(t) = g(t) . 어떤 함수를 델타함수와 컨벌루션하면 그 함수는 아무런 변화가 없음 ㅇ 푸리에 변환 쌍 - δ(t) ↔ 1 . 시간영역의 델타함수는 전체 주파수 영역에서 스펙트럼 특성이 균일함 ㅇ 계단함수의 도함수는 임펄스함수가 됨
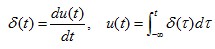
▷신호 파형 종류
1. 정현 신호 2. 지수 신호 3. 삼각 함수 4. 계단 신호 5. 램프 신호 6. 임펄스 신호 7. 삼각 펄스 신호 8. 구형 펄스 신호 9. 싱크 신호 10. 특이 함수 11. 기초 이산 신호 12. 복소 지수 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]