Time Scaling 시간 스케일링, 시간 비율변화, 시간 척도 조절, 시간 척도 변환 | (2022-07-15) |
Down Sample, Down-sampling, 다운 샘플링, Decimation, 데시메이션, Decimator, Up Sample, Up-sampling, 업 샘플링 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
이산 신호/이산 시스템
▷
이산 신호, 이산 연산
1. 시간 스케일링, 시간 비율변화, 시간 척도조절 (Time Scaling) ㅇ 시간 변수 t에 어떤 숫자를 곱하거나 나누면, - 파형 모양이 옆으로 수축 혹은 퍼지는 효과를 말함 - 例) |a|>1 일때, . y(t) = x(at) => 신호의 길이를 감소시키며 수축 . y(t) = x(t/a) => 신호의 길이를 증가시키며 확장2. (신호처리 관점) 샘플링율 변화에 의한 시간 척도 조절 ㅇ 다운 샘플링 / 데시메이션 (Down-samping / Decimation) - 실제 보다 더 띄엄띄엄 샘플을 얻음 . 수축된 신호를 얻게되나, 일부 정보를 잃어버림 - 신호의 길이를 줄임 => 수축 효과 (원 신호가 응축되는 효과) . 시간이 감에 따라 빨라지며 수축되는 효과 . 예) 원래 녹음된 것 보다 더 빠르게 재생되는 테이프 ㅇ 업 샘플링 / 보간 (Up-sampling / Interpolation) - 실제 보다 더 많은 샘플을 얻음 . 인접한 샘플들 사이에 0 값 샘플들을 삽입시키는 등 . 이산시간 신호를 시간에 따라 확장시키는 것 - 신호의 길이를 늘림 => 확장 효과 (원 신호가 늘어지는 효과) . 시간이 감에 따라 천천히가며 확장되는 효과 . 예) 정상속도 보다 낮은 속도로 재생되는 테이프 3. (푸리에 변환 관점) 시간 - 주파수 상반 관계 ㅇ 푸리에 변환 성질 ☞ 푸리에 변환 역변환 관계 참조
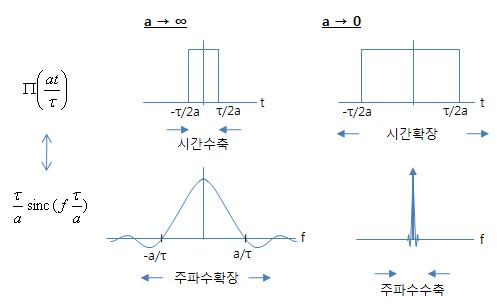
- (시간 수축 ↔ 주파수 확장), (시간 확장 ↔ 주파수 수축) . 즉, `수축성`,`확장성`이 변환영역 간에 서로 상반적임 - 例) 사각파
▷이산 신호, 이산 연산
1. 이산 신호 2. 이산 신호 표현 3. 디지털 주파수 4. 기초 이산 신호 5. 기초 이산 연산 6. 시간 스케일링 7. 윈도잉 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]