Karnaugh Map 카르노 맵 | (2022-01-05) |
K–Map | |
▷
Top
▷
전기전자공학
▷
디지털공학
▷
부울 대수
1. 카르노 맵 ㅇ 복잡한 논리식을 도식화시켜, 이를 통한 체계적인 축소 과정을 시각적으로 보여주며, 간략화시킨 등가식으로 만듬 ※ 1953년 벨연구소의 모리스 카르노(Maurice Karnaugh)에 의해 소개됨 2. 카르노 맵의 특징 ㅇ 논리표의 관찰에 의해, 논리적으로 인접한 관계를 위치적으로 인접한 관계로 변환시켜 간략화 도모 ㅇ 주어진 논리함수에서, 최소항(Minterm)들을 결합시켜, 최소 비용으로 논리회로를 구현 ㅇ 최소 축약 여부를 비교적 쉽게 판단 가능 ㅇ 4개까지의 변수를 갖는 부울식에서 비교적 잘 작동 - (특히, 간단한 수기 및 통찰력에 도움을 줌) 3. 카르노맵에서 논리 `1`들의 묶음 규칙 ㅇ 바로 이웃한 항 끼리 묶음 (looping) ㅇ 정사각형,직사각형 형태로 가능한 크게 묶고 그 수를 최소화시킴 ㅇ 가로,세로 방향으로 2의 거듭제곱(1,2,4)개의 사각형 블록화 ㅇ 여러 묶음이 겹쳐 나타날 때에 개별적인 묶음은 OR로 묶음 ※ 3 부울변수 例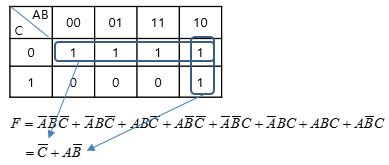
▷부울 대수
1. 부울 대수 2. 부울변수,부울식,부울함수 3. 드모르간의 법칙 4. 진리값,진리표 5. 부울 대수의 주요 정리들 6. 부울식의 간략화 7. 카르노 맵 8. 퀸 맥클러스키 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]